《程序员的数学》思考题(一)

《程序员的数学》这本书,除了前两章介绍数学的基本概念外,其它章节主要通过思考题的方式,在解答过程中给我们讲解数学知识和思维方式。所以看完整本书后,通过对思考题的不断训练 ,可以使我们串起书中的知识点,巩固知识。为了便于日后的复习,这里整理了书中绝大多数的思考题,内容舒适,请放心食用。
ps:答案只有结果,不包含解答过程。
// -================= Let’s Begin =================
P64:今天是星期日,那么100天以后是星期几?
**答:**星期二。
P66:今天是星期日,那么10^100天以后是星期几?
**答:**星期四。
P70:1234567^987654321的个位数是什么?
答: 7。
P71:棋子魔术
魔术师和他的徒弟在台上表演,下面有3位观众。魔术师蒙着眼睛。
(1)桌上随机排列着7个黑白棋的棋子(图3-4)。魔术师蒙着眼睛,看不到棋子。
 (2)魔术师的徒弟看完这7枚棋子之后,又往右面添了一枚棋子,与其他棋子并排,这时则有8枚棋子(图3-5)。魔术师依然蒙着眼睛。
(2)魔术师的徒弟看完这7枚棋子之后,又往右面添了一枚棋子,与其他棋子并排,这时则有8枚棋子(图3-5)。魔术师依然蒙着眼睛。
 (3)这时观众可将其中的1枚棋子翻转,或不翻转任何棋子(图3-6)。
(3)这时观众可将其中的1枚棋子翻转,或不翻转任何棋子(图3-6)。
 (4)魔术师摘下眼罩,观察8枚棋子,然后马上就能说出“观众翻转了棋子”或“没有翻转棋子”,识破观众的行为。
(4)魔术师摘下眼罩,观察8枚棋子,然后马上就能说出“观众翻转了棋子”或“没有翻转棋子”,识破观众的行为。
 魔术师是如何识破观众的行为的呢?
魔术师是如何识破观众的行为的呢?
答: 徒弟在观众摆放的7枚棋子中,数出黑棋的个数。如果黑棋数是奇数,就添黑棋。如果黑棋数是偶数,就添白棋。不管哪种情况,在最终的8个棋子中,黑棋必为偶数个。 观众的行为可以是以下(1)~(3)三种情况之一。 (1)观众翻转白旗。那么,黑棋就增加了1枚,即黑棋变为奇数个。 (2)观众翻转黑棋。那么,黑棋就减少了1枚,黑棋也变为奇数个。 (3)观众不翻转棋子。黑棋仍然是偶数个。 魔术师摘下眼罩,马上数出黑棋的个数。如果黑棋为奇数个,就说“观众翻转了棋子”。如果为偶数个,就说“没有翻转棋子”。 这里,徒弟摆放棋子使“黑棋个数为偶数”。若使“黑棋个数为奇数”也可以,只要魔术师和徒弟事先商量好就行。
P74:寻找恋人
在一个小王国中,有8个村子(A~H)。如图3-8所示,各个村子之间有道路相连(黑点表示村子,线表示道路)。而你要寻找流浪在这个王国的你唯一的恋人。
你的恋人住在8个村子中的某一个里。她每过1个月便顺着道路去另一个村子,每个月都一定会换村子,然而选择哪个村子是随机的,预测不了。例如,如果恋人这个月住在G村,那么下个月就住在“C、F、H中的某个村子”。
目前你手头上掌握的确凿信息只有:1年前(12个月前),恋人住在G村。请求出这个恋人住在A村的概率。
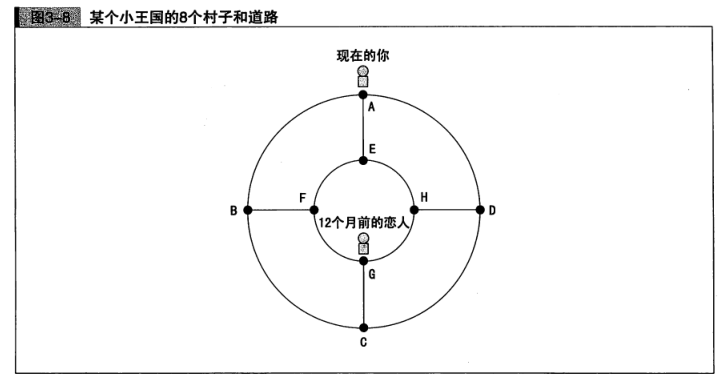
**答:**概率为0。
P77:铺设草席
如图3-11所示,有这样一个房间。使用图中右下角所示的草席能够正好铺满房间吗?前提是不能使用半张草席。
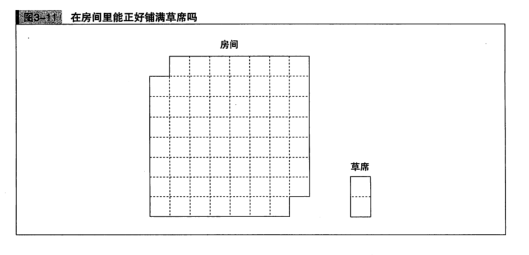
**答:**不能。
P79:哥尼斯堡七桥问题
在很久以前,有一个叫哥尼斯堡的小城。小城被河流分割成了4块陆地。人们为了连接这些陆地,建设了7座桥(图3-13)。
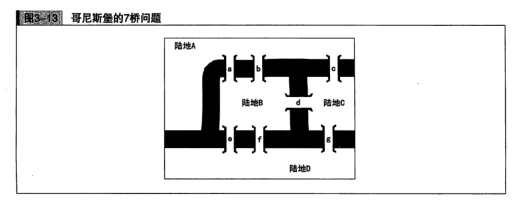 现在你要找出走遍7座桥的方法。但是,必须遵守以下条件:
现在你要找出走遍7座桥的方法。但是,必须遵守以下条件:
- 走过的桥不能再走。
- 可以多次经过同一块陆地。
- 可以以任一块陆地为起点。
- 不需要回到起点。
最后,如果能够走遍7座桥的话,请说明一下方法。如果不能的话,也请说明一下。
答:
 不能走遍哥尼斯堡七桥。
不能走遍哥尼斯堡七桥。
P88:存钱罐的钱
在你面前有一个空存钱罐。
- 第 1 天,往存钱罐里投入 1 元。存钱罐中总金额为 1 元。
- 第 2 天,往存钱罐里投入 2 元。存钱罐中总金额为 1 + 2 = 3 元。
- 第 3 天,往存钱罐里投入 3 元。存钱罐中总金额为 1 + 2 + 3 = 6 元。
- 第 4 天,往存钱罐里投入 4 元。存钱罐中总金额为 1 + 2 + 3 + 4 = 10 元。
那么,每天都这样往存钱罐里投入硬币的话,第 100 天时的总金额为多少呢?
答: 5050元。
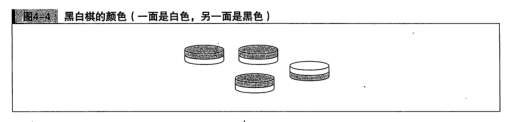
P99:黑白棋子的颜色
黑白棋一面是白色,一面是黑色。现在,我们往棋盘上随便仍几枚棋子。有时会碰巧都是白色或都是黑色。但有时既有白棋,也有黑棋。
 使用数学归纳法可以“证明”投掷的黑白棋的颜色一定相同。然而现实中这却是不可能的。
那么,请找出下述“证明”中的错误之处。
假设n为1以上的整数,用数学归纳法证明以下断言T(n)对于1以上的所有整数n都成立。
使用数学归纳法可以“证明”投掷的黑白棋的颜色一定相同。然而现实中这却是不可能的。
那么,请找出下述“证明”中的错误之处。
假设n为1以上的整数,用数学归纳法证明以下断言T(n)对于1以上的所有整数n都成立。
- 断言T(n):投掷n枚黑白棋,所有棋子的颜色一定相同。
步骤1:基底的证明 证明T(1)成立。 断言T(1)即“投掷1枚黑白棋子时,所有棋子的颜色一定相同”。棋子只有1个,颜色当然只有1种,因此T(1)成立。 这样,步骤1就得到了证明。
步骤2:归纳的证明
证明当k为1以上的任意整数时,“若T(k)成立,则T(k+1)也成立”。
首先假设“投掷k枚黑白棋子时,所有棋子的颜色一定相同”成立。现假设投掷k枚棋子后,再投掷一枚黑白棋。那么投掷的棋子总数为k+1枚。
这里,将投掷的棋子以每k枚为单位分为两组,分别将这两组称为A和B(图4-5)。
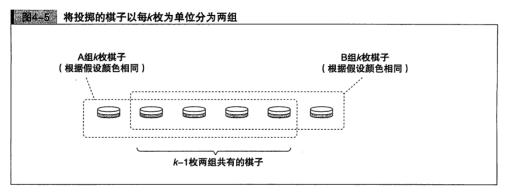 因为“投掷k枚黑白棋子时,所有棋子的颜色一定相同”的假设成立,所以A组的棋子(k枚)和B组的棋子(k枚),分别都是相同色。而通过图4-5可见,两组共有的棋子为k-1枚。因为各组的棋子颜色相同,又有两组共有的棋子,所有k+1枚棋子颜色相同。这就是断言T(k+1)。
这样,步骤2就得到了证明。
通过数学归纳法,证明了断言T(n)对于1以上的所有整数n都成立。这个证明有什么不对的地方呢?
因为“投掷k枚黑白棋子时,所有棋子的颜色一定相同”的假设成立,所以A组的棋子(k枚)和B组的棋子(k枚),分别都是相同色。而通过图4-5可见,两组共有的棋子为k-1枚。因为各组的棋子颜色相同,又有两组共有的棋子,所有k+1枚棋子颜色相同。这就是断言T(k+1)。
这样,步骤2就得到了证明。
通过数学归纳法,证明了断言T(n)对于1以上的所有整数n都成立。这个证明有什么不对的地方呢?
答:
步骤1没有问题。若棋子只有1枚,那么就只有1种颜色。
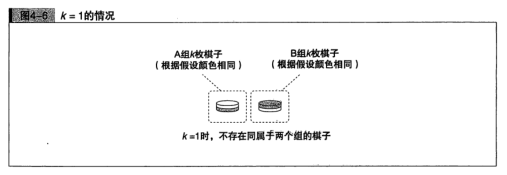
问题在步骤2的图(图4-5)中。实际上,该图在k=1时不成立。k=1时,两组棋子分别都只有1枚。双方共有的棋子为k-1枚,而k-1=0,所有不存在同属于两个组的棋子(图4-6)。
 因此在数学归纳法的两个步骤中,步骤2是无法得到证明的。
因此在数学归纳法的两个步骤中,步骤2是无法得到证明的。
P111:植树问题
在10米长的路上,从路的一端起每隔1米种一棵树,那么需要种多少颗树?
答: 11棵。
P112:最后的编号
内存中排列着程序要处理的100个数据。从第1个开始顺次编号为0号、1号、2号、3号……那么,最后1个数据的编号是多少?
答: 99号。
P115:加法法则
在一副扑克牌中,有10张红桃数字牌(A、2、3、4、5、6、7、8、9、10),3张红桃花牌(J、Q、K)。那么红桃共有多少张?
答: 13张。
P115:控制亮灯的扑克牌
在一副扑克牌中,有13个级别(A、2、3、4、5、6、7、8、9、10、J、Q、K)。这里,我们分别将A、J、Q、K设为整数1、11、12、13。
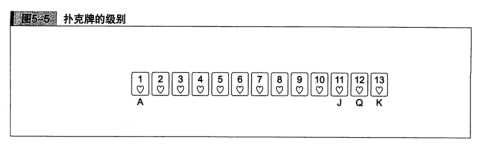 在你面前有一个装置,只要往里面放入1张牌,它就会根据牌的级别控制灯泡的亮灭。我们假设放入的扑克牌的级别为n(1~13的整数),
在你面前有一个装置,只要往里面放入1张牌,它就会根据牌的级别控制灯泡的亮灭。我们假设放入的扑克牌的级别为n(1~13的整数),
- 若n是2的倍数,则亮灯。
- 若n是3的倍数,也亮灯。
- 若n既不是2的倍数,也不是3的倍数,则灭灯。
往这个装置中依次放入13张红桃,其中亮灯的有多少张牌呢?
答: 8张。
P117:乘法法则
在一副扑克牌中,有红桃、黑桃、方片、梅花四种花色。每个花色都有A、2、3、4、5、6、7、8、9、10、J、Q、K这13个等级。那么,一副扑克牌共有多少张?(这里除去王牌)
答: 52张。
P119:3个骰子
将3个写有数字1到6的骰子并列放置,形成一个3位数,共能形成多少个数字?
答: 216个。
P120:32个灯泡
1个灯泡有亮和灭2种状态。若将32个这样的灯泡排成一排,则共有多少种亮灭模式。
答: 4294967296种。
P121:3张牌的置换
如果将A、B、C这3张牌按照ABC、ACB、BAC……等顺序排列,那么共有多少种排法?
答: 6种。
P123:扑克牌的置换
将一副扑克牌里的52张(不包括王牌)摆成一列,共有多少种摆法?
答: 52!(52的阶乘)
P125:从5张扑克牌中取出3张进行排列
你现在手上持有A、B、C、D、E共5张牌。要从这5张牌中取出3张牌进行排列。请问有多少种排法?
答: 60种。
P134:药品调剂
现假设要将颗粒状的药品调剂成一种新药。药品有A、B、C三种。新药调剂规则如下。
- 从A、B、C这3种药品中,共取100粒进行调剂。
- 调剂时,A、B、C这3种药品每种至少有1粒。
- 不考虑药品调剂的顺序。
- 同种药品每粒都相同。
这种情况下,新药调剂的组合共有多少种?
答: 4851种
P136:至少有一端是王牌
现在有5张扑克牌,其中王牌2张,J、Q、K各1张。将5张牌排成一排,左端或右端至少有一端是王牌的排法有多少种?(不区分大小王牌)
答: 42种。
